介绍拉格朗日乘子法及其推广KKT条件,以及它们在PCA和SVM中的应用
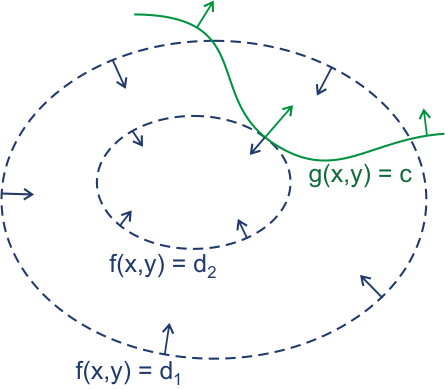
图片来自wikipedia关于拉格朗日乘子法的形象介绍
拉格朗日乘子法
- 拉格朗日乘子法是一种求约束条件下极值的方法,描述为
$$
在约束条件g(x,y)=c下 \
求函数f(x,y)的极值 \
$$
其主要思想是将约束条件和原函数合成一个函数,转换为无约束条件,进而求偏导得到极值。 - 由图可以看出,f函数值相等的点可以构成类似等高线的蓝色环,约束条件是绿色的路径。问题可以转换为,我们沿着绿色路径走,走到哪一点时这个点所在的蓝色环最靠中心或者最靠外沿(极大极小值)。
- 显然,在绿色路径与蓝色环相切的点取得极值,此时它们的梯度(箭头)平行,描述为
$$
\nabla f (x, y) = \nabla (\lambda \left(g \left(x, y \right) - c \right))
$$
$\lambda$是拉格朗日乘数,在这个式子中代表两个平行梯度的大小倍数,正负代表两个梯度方向相反。拉格朗日乘数不为0。
拉格朗日方程即$ F(x,y)=\nabla \Big[f \left(x, y \right) + \lambda \left(g \left(x, y \right) - c \right) \Big] $ - 求解上面的式子,就得到一组$(x,y,\lambda)$,即极值点和达到极值时的拉格朗日乘数。此时拉格朗日方程$F(x,y)=f(x,y)$,因为取得极值时约束条件部分一定为0(我们是沿着约束条件走找相切点,相切点在约束路径上)。
- 拉格朗日系数的含义是最大增长值,$-\frac{\partial \Lambda}{\partial {c_k}} = \lambda_k$
卡罗需-库恩-塔克条件
- 如果约束条件不仅仅是等式,还包括不等约束条件,这就需将拉格朗日乘子法推广到KKT条件
- 包含不等约束的极值问题描述为
$$
在约束条件: \
h_j(X)=0 j=1,2,…,p \
g_k(X)\leq 0 k=1,2,…q \
求函数f(X)的极值 \
$$ - 拉格朗日函数为
$$
L(X,\lambda ,\mu)=f(X)+\sum _{j=1}^p \lambda _j h_j(X) + \sum _{k=1}^q \mu g_k(X)
$$ - KKT条件为:
$$
\frac{dL}{dX}=0 \
\lambda _j \neq 0 \
\mu _k \geq 0 \
\mu _k g_k(X)=0 \
h_j(X)=0 \
g_k(X) \leq 0\
$$
PCA
- PCA即Principal Component Analysis,主成分分析,将数据原本的维度进行优化,形成一组新的维度,它们是原有维度的线性组合且互不相关,按重要性大小排序,一个维度可以理解为数据矩阵中一列,一行代表一个样本
- 记$x_1,…,x_p$为原始p个维度,新维度是$\xi _1,…,\xi _p$
- 新维度是原始维度的线性组合,表示为
$$
\xi _i = \sum _{j=1}^{p} \alpha _{ij} x_j = \alpha _i^T x
$$ - 为了各个新维度统一尺度,另每个新维度的线性组合系数的向量长度都为1,即
$$
\alpha _i^T \alpha _i=1
$$ - 令A为特征变换矩阵,由各个新维度的线性组合系数向量构成,则需要求解一个最优的正交变换A,使得新维度的方差达到极值。其中正交变换即保证各个新维度不相关,方差越大则样本在新维度上具有区分度,方便我们进行数据的分类
- 此时问题就转化为具有约束条件的极值问题,约束条件为$\alpha _i^T \alpha _i=1$,求$var(\xi _i)$的极值,可以用拉格朗日乘子法求解
- 当i=1时,我们求出来第一个也是重要性最大(方差最大)的新维度,再令i=2,并加入约束条件$E[\xi _2 \xi _1-E[\xi _1][\xi _2]]=0$即两个新维度不相关,求出第二个新维度
- 依次求出p个新维度
- PCA能够优化原始数据,找出具有区分度的维度,更重要的是如果原始数据的维度存在相关性,PCA能消除这些相关性,即便原始数据相关性很低,如果我们只取前k(k<q)个新维度,就可以在损失较小精确度的情况下进行降维,大大缩短数据的训练时间
- 如果我们取了前k个新维度,再对他们进行PCA的逆运算,就可以实现数据的降噪,因为重要性很低的新维度一般反应了数据中的随机噪声,抛弃它们并恢复原始数据时就实现了噪音的去除
- PCA是非监督的,没有考虑样本本身的类别或者标签,在监督学习中不一定是最优解,可以利用K-L变换实现针对分类的目标进行特征提取
PCA using Covariance Matrix
- 上述求解PCA的方法太过于麻烦,在实际中可以通过协方差矩阵来求解(因为有高效的矩阵特征分解算法)
- PCA的优化目标是,重新选取一组基(特征),使得数据在这组基表示下,不同特征之间的协方差为0,同一特征内的数据方差最大化
- 可以将问题转述为,对数据张量X,按特征列(共m个特征)零均值化(化简协方差的计算),计算协方差矩阵$C=\frac 1m X^T X$,希望求得一组基P,使得特征变换后的数据$Y=PX$的协方差矩阵D是对角阵,非对角元素(协方差)为0.若对角元素(方差)按从大到小排列,这时我们取P矩阵的前k行就可以将特征维度从m降到k。易得$D=PCP^T$,且C为实对称阵,那么问题就转变为对实对称C对角化,我们需要的新的一组基就是特征向量组。
- 算法:
- 有m条n维数据,排成n行m列矩阵X
- 将X的每一行进行零均值化
- 求出协方差矩阵C
- 求出协方差矩阵的特征值和特征向量
- 将特征向量按特征值大小对应从大到小按行排列,组成新的基矩阵P
- 如果需要将为,取P的前k行即可,降维后的数据为$Y=PX$
1 | def PCA(X, dims): |
SVM
- 在分类学习中,我们需要找到一个划分超平面,将不同类别的样本分开,而最好的划分超平面显然是离所分各个样本类尽量远,即对训练样本局部扰动容忍性最好的超平面
- 划分超平面通过方程$w^Tx+b=0$描述,其中w为法向量,决定了超平面方向,b为超平面到远点的位移
- 求解一个SVM,即找到满足约束
$$
\begin{cases}
w^Tx_i+b \geq +1, y_i=+1 \
w^Tx_i+b \leq -1, y_i=-1 \
\end{cases}
$$
的条件下,使得两个异类支持向量到超平面的距离$\frac{2}{||w||}$最大
这可以重写为最优化问题
$$
min_{w,b} \frac 12 {||w||}^2 \
s.t. y_i(w^Tx_i+b) \geq 1,i=1,2,…,m \
$$
推导见另两篇博文:机器学习笔记和统计学习方法笔记手写版 - 对于这个最优化问题,它的拉格朗日方程是
$$
L(w,b,\alpha )=\frac 12 {||w||}^2+\sum _{i=1}^{m} \alpha _i (1-y_i(w^Tx_i+b))
$$
其中$\alpha$是拉格朗日乘子,令方程分别对w,b求偏导,得到对偶问题
$$
max _{\alpha } \sum _{i=1}^m \alpha _i -\frac 12 \sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j x_i^T x_j \
s.t. \sum _{i=1}^m \alpha _i y_i=0, \
\alpha _i \geq 0,i=1,2,…,m \
$$
上式满足KKT条件,通过SMO算法求解